Faire la même application avec Rshiny a été plutot facile. L’app reste extremement simple c’est vrai, mais la structure des DashBoards est en fait commune entre tout les outils.

Il y toujour le layout, dans lequel on va déclarer tous les éléments qui composeront la page. Et ensuite la partie réactive qui correspond aux callbacks de Dash. C’est la qu’on désigne les élements dont il faut suivre le contenu, et déclencher des calculs en conséquence.

Dans Shiny on a le server et Dash les callbacks!, ce qui rend les compétences d’un outil plutot transférables. De plus, Dash peut être appellé de python, R ou julia, ce qui permet d’utiliser les aides et forums d’une grande comunautée. Cependant, lorsqu’on est face a des problèmes spécifiques et que l’on veut comprendre la source des outils Dash, la source julia n’est pas compréhensible, vu que c’est du code auto-généré.

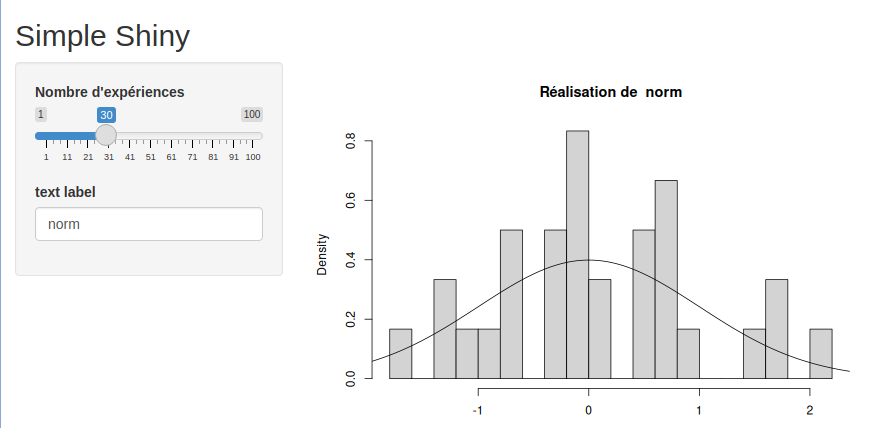Comme le montre cette source:

function generate_component!(block, module_name, prefix, meta)
    args = isempty(meta["args"]) ? Symbol[] : Symbol.(meta["args"])
    wild_args = isempty(meta["wild_args"]) ? Symbol[] : Symbol.(meta["wild_args"])
    fname = string(prefix, "_", lowercase(meta["name"]))
    fsymbol = Symbol(fname)

    append!(block.args,
            (quote
                export $fsymbol
                function $(fsymbol)(;kwargs...)
                    available_props = $args
                    wild_props = $wild_args
                    return Component($fname, $(meta["name"]), $module_name, available_props, wild_props; kwargs...)
                end
            end).args
    )
    signatures = String[string(repeat(" ", 4), fname, "(;kwargs...)")]
    if in(:children, args)
        append!(block.args,
            (quote
                $(fsymbol)(children::Any; kwargs...) = $(fsymbol)(;kwargs..., children = children)
                $(fsymbol)(children_maker::Function; kwargs...) = $(fsymbol)(children_maker();kwargs...)
            end).args
        )
    push!(signatures,
            string(repeat(" ", 4), fname, "(children::Any, kwargs...)")
        )
    push!(signatures,
            string(repeat(" ", 4), fname, "(children_maker::Function, kwargs...)")
        )
    end
    docstr = string(
        join(signatures, "\n"),
        "\n\n",
        meta["docstr"]
    )
    push!(block.args, :(@doc $docstr $fsymbol))
end

qui est la fonction qui génère les dcc_components utilisés pour déclarer les éléments du layout html.

Esprit

On peut déja constater une différence notable dans la manière de programmer les fonctions liées aux probabilités. Car dans R chaque lois a ses propres fonctions:

    - de génération r<loi>
    - de densité d<loi>
    - de fonction de répartition p<loi>
    - de quantile q<loi>

Alors de qu’en julia on peut utiliser rand() pdf(), cdf() et quantile() qui vont changer de comportement en fonction des distributions qu’on leur donnera. Cela rend le code plus clair et générique.

using Distributions
using StatsPlots

function plot_hist(d::Distribution,n::Int = 1000)

        p = histogram(rand(d,n))
        plot!(d) # pdf par defaut

        return p
end
evalf = function(s,t){
  eval(parse(text=paste(s,t,sep="")))
}

plot_hist = function(d, n){
  x = seq(-5,5,by=0.1)
  loi = evalf("r",d)
  loi_pdf = evalf("d",d)
  
  
  hist(loi(n),
       breaks = 25,
       freq = FALSE)
  
  lines(x,loi_pdf(x))
}
import scipy
import matplotlib.pyplot as plt 
import numpy as np

def plot_hist(d,n, *args):
     loi = eval(f"scipy.stats.{d}{args}.rvs")
     loi_pdf = eval(f"scipy.stats.{d}{args}.pdf") 
 
     x = np.linspace(min(loi(n)),max(loi(n))+1,1000)

     plt.hist(loi(n), density = 1)
     plt.plot(x,loi_pdf(x))
     plt.title(f"Réalisation et densité de loi {d} de parametres  {args}")
Code 
evalf = function(s,t){
  eval(parse(text=paste(s,t,sep="")))
}

plot_hist = function(d, n){
  x = seq(-5,5,by=0.1)
  loi = evalf("r",d)
  loi_pdf = evalf("d",d)
  
  
  hist(loi(n),
       breaks = 25,
       freq = FALSE)
  
  lines(x,loi_pdf(x))
}
plot_hist("norm", 100)

Code 
import scipy
import matplotlib.pyplot as plt 
import numpy as np

def plot_hist(d,n, *args):
     loi = eval(f"scipy.stats.{d}{args}.rvs")
     loi_pdf = eval(f"scipy.stats.{d}{args}.pdf") 
 
     x = np.linspace(min(loi(n)),max(loi(n))+1,1000)

     plt.hist(loi(n), density = 1)
     plt.plot(x,loi_pdf(x))
     plt.title(f"Réalisation et densité de loi {d} de parametres  {args}")
plot_hist("norm", 300, 1,2)
plt.show()

On voit qu’en deux lignes on a pu généraliser le processus de création de graphique de simulation. Grace a l’abstraction rendue possible par les fonctions rand et plot(version de Statsplots).

Ici je ne sais pas si l’exemple était si pertinent car pour avoir une fonction exactement identique il aurait fallut dévelloper de nouveaux types pour modéliser les distributions.