Code
using StatsPlots
using Distributions
using DataFrames
plot(Beta(3,7), label = "Beta(3,7)", size = (1000,800), title = "3 faces et 7 piles")
plot!(Normal(0.5,0.25), label = "Théorique")
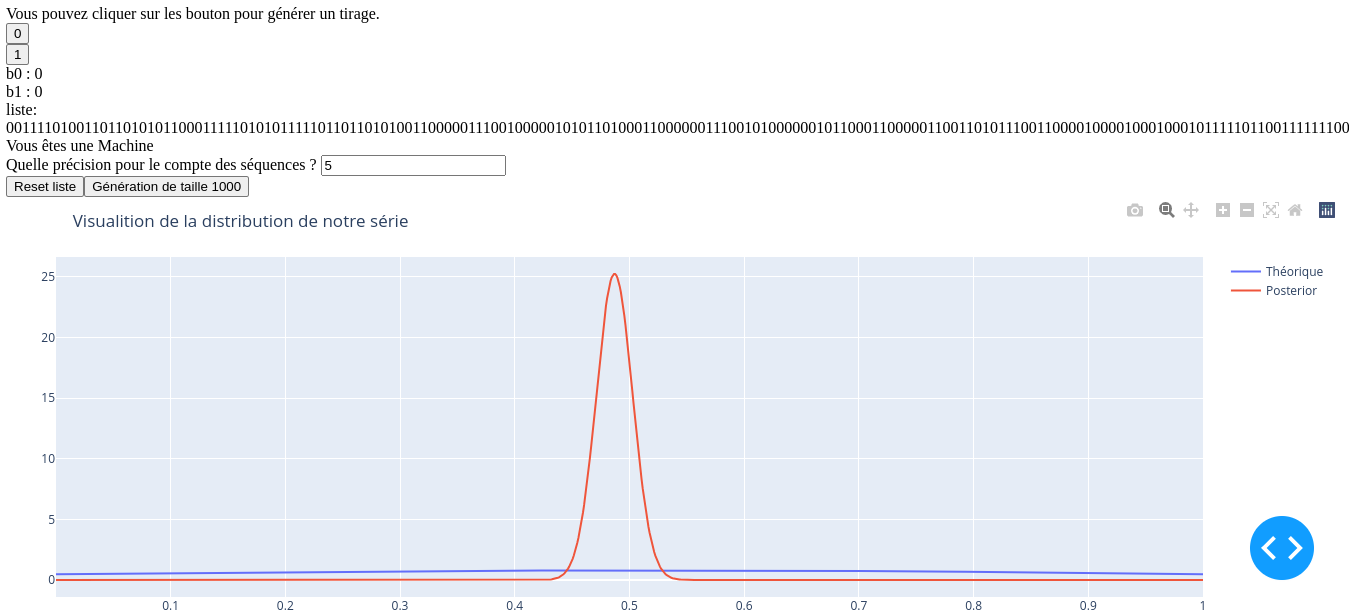
xlims!(0,1)Comme précisé dans la page de présentation, j’ai ici essayé de réaliser un test de turing inversé. Il s’agit d’une application plutot simple qui permet à l’utilisateur d’essayer de générer aléatoirement des 0 et des 1 de manière à ressembler à un vrai tirage aléatoire. L’application lui trace en direct l’histogramme de ses réalisations et le graph du postérieur bayésien (Loi Béta) associé à ces tirages.
On peut aussi générer de vrais nombres pseudo-aléatoires pour observer à quoi ressemble une vrai suite.
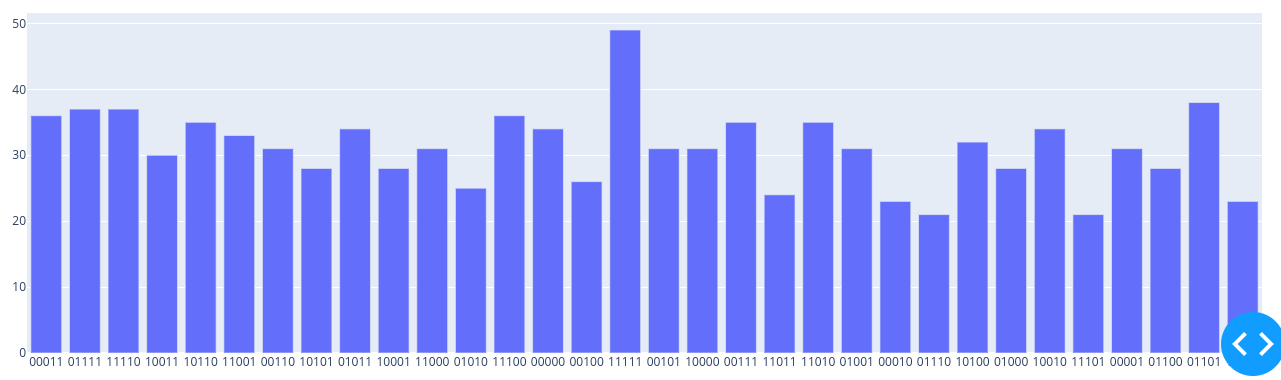
L’histogramme est modulable est permet d’observer la répartition de chaque taille de sous-séquence de 0 et de 1 car dans un cas vraiment aléatoire, n’importe quelle sous-séquence est uniformément présente. Et on voit que lorsque l’humain génère des nombres aléatoires, il y a beaucoup plus d’alternances que lors d’un vrai tirage.
Aussi on a un z-test naif qui détecte si la source de la séquence est un humain ou une machine, avec H0 machine.
---
title: Inverse turing
---
Comme précisé dans la page de présentation, j'ai ici essayé de réaliser un test de turing inversé.
Il s'agit d'une application plutot simple qui permet à l'utilisateur d'essayer de générer aléatoirement
des 0 et des 1 de manière à ressembler à un vrai tirage aléatoire.
L'application lui trace en direct l'histogramme de ses réalisations et le graph du postérieur bayésien (Loi Béta) associé à
ces tirages.
On peut aussi générer de vrais nombres pseudo-aléatoires pour observer à quoi ressemble une vrai suite.
L'histogramme est modulable est permet d'observer la répartition de chaque taille de sous-séquence de 0 et de 1
car dans un cas vraiment aléatoire, n'importe quelle sous-séquence est uniformément présente.
Et on voit que lorsque l'humain génère des nombres aléatoires, il y a beaucoup plus d'alternances que lors d'un vrai tirage.


quarto-executable-code-5450563D
```julia
using StatsPlots
using Distributions
using DataFrames
plot(Beta(3,7), label = "Beta(3,7)", size = (1000,800), title = "3 faces et 7 piles")
plot!(Normal(0.5,0.25), label = "Théorique")
xlims!(0,1)
```
Aussi on a un z-test naif qui détecte si la source de la séquence est un humain ou une machine, avec H0 machine.